Гидравлический диаметр
Гидравлический (эквивалентный) диаметр — мера эффективности русла в пропускании потока жидкости, равняется такому диаметру трубы, которая будет создавать эквивалентное сопротивление потоку, что и русло с площадью сечения потока и смоченным периметром . Чем меньше гидравлический диаметр, тем бо́льшее сопротивление потоку оказывает русло (при одинаковой площади поперечного сечения потока).
Нахождение
Определяется по формуле:
где A — площадь поперечного сечения потока жидкости и P — смоченный периметр (см. ниже) поперечного сечения потока.
1) Для трубы круглого поперечного сечения, полностью (без пустот) заполненной жидкостью, эта формула принимает вид:
То есть, для круглого сечения гидравлический диаметр равен геометрическому диаметру.
2) Для кольца гидравлический диаметр равен:
где — наружный диаметр кольца, — внутренний диаметр кольца.
3) Для каналов прямоугольного сечения гидравлический диаметр определяют по формуле:
где a — уровень заполнения канала и b — ширина канала.
Смоченный периметр
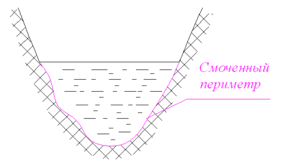
Смоченный периметр — длина части границы канала, касающейся жидкости.
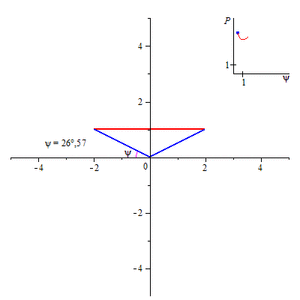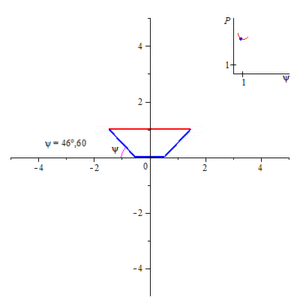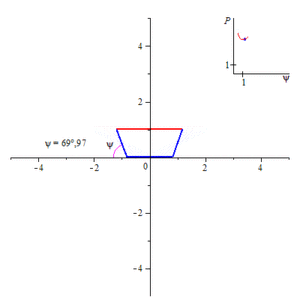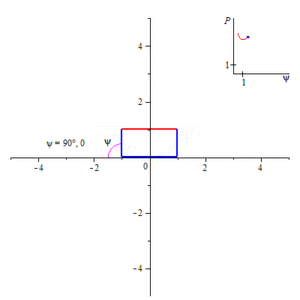
Понятие смоченного периметра имеет большое значение при проектировании каналов. Расход воды равен произведению площади поперечного сечения канала на скорость течения. Скорость же течения, по формуле Шези, при постоянной площади сечения канала и гидравлическом уклоне, прямо пропорциональна квадратному корню из гидравлического радиуса, то есть обратно пропорциональна квадратному корню из смоченного периметра. Поэтому при заданной площади поперечного сечения стараются минимизировать смоченный периметр, чтобы увеличить скорость течения, а, следовательно, и расход воды. Поперечное сечение канала обычно представляет собой равнобедренную трапецию, нижнее основание которой меньше верхнего. Смоченный периметр такого канала равен сумме нижнего основания и боковых сторон этой трапеции. Считая площадь такой трапеции заданной, находят минимум смоченного периметра в зависимости либо от угла откоса (угол, смежный углу при нижнем основании) при постоянной глубине (то есть высоте трапеции), либо от глубины при постоянном угле откоса. В первом случае наименьший смоченный периметр будет при угле откоса, равном 60°[1].
Гидравлический радиус
Существует также понятие «гидравлический радиус». Несмотря на своё название, гидравлический диаметр не равен двум гидравлическим радиусам.
Гидравлический радиус вычисляется по формуле:
- ,
где:
- A — площадь поперечного сечения (м²)
- P — смоченный периметр (м)
См. также
Примечания
- ↑ Попов Г.Н. Как применялась и применяется тригонометрия на практике. — 2-е изд. — Государственное учебно-педагогическое издательство, 1931. — С. 73—82. — 88 с. — (Рабочая библиотека по математике для школ II ступени). Архивировано 26 июня 2013 года. Архивированная копия. Дата обращения: 17 ноября 2016. Архивировано 26 июня 2013 года.
Литература
- Ю. И. Дытнерский. Процессы и аппараты химической технологии. Часть 1. Теоретические основы процессов химической технологии. — М.: Химия, 1995. — 400 с. — 6500 экз. — ISBN 5-7245-1006-5.

















