Масса

Масса
${\displaystyle M,m}$
Размерность	M
Единицы измерения
СИ	кг
СГС	г

Ма́сса — скалярная физическая величина, определяющая инертные и гравитационные свойства тел в ситуациях, когда их скорость намного меньше скорости света^[1]. В обыденной жизни и в физике XIX века масса синонимична весу^[2].

Будучи тесно связанной с такими понятиями механики, как «энергия» и «импульс», масса проявляется в природе двумя качественно разными способами, что даёт основания для подразделения её на две разновидности:

• инертная масса характеризует инертность тел и фигурирует в выражении второго закона Ньютона: если заданная сила в инерциальной системе отсчёта одинаково ускоряет различные тела, им приписывают одинаковую инертную массу;
• гравитационная масса (пассивная и активная) показывает, с какой силой тело взаимодействует с внешними полями тяготения^[3] и какое гравитационное поле создаёт само это тело^[4], она входит в закон всемирного тяготения и положена в основу измерения массы взвешиванием.

Однако экспериментально с высокой точностью установлена пропорциональность гравитационной и инертной масс^[5][6], и подбором единиц они сделаны в теории равными друг другу. Поэтому, когда речь не идёт об особой «новой физике», принято оперировать термином «масса» и использовать обозначение m без пояснений.

Массой обладают все макроскопические объекты, бытовые предметы, а также большинство элементарных частиц (электроны, нейтроны и др.), хотя среди последних имеются и безмассовые (например, фотоны). Наличие массы у частиц объясняется их взаимодействием с полем Хиггса.

Величина массы входит в нерелятивистское выражение второго закона Ньютона F = ma, дающее связь между силой и вызываемым ею ускорением свободного тела. Указанный закон, одновременно с утверждением линейности соотношения «сила—ускорение», по сути, выступает определением инертной массы. Сила при этом определяется логически независимо и от закона Ньютона, и от понятия «ускорение»^[7]: она равна деформации специальной тестовой пружины (с точностью до калибровочного множителя).

Масса может измеряться в килограммах. Официальным эталоном массы «1 кг» по 2018 год служил конкретный объект (см. фото выше); по соглашению, если приложенная к эталону сила обеспечивает ускорение 1 м/с², то такая сила имеет величину 1 Н. Данным соглашением задаётся единичная сила — приложив её к упомянутой пружине, можно прокалибровать последнюю и использовать для измерений. Инертная масса любого исследуемого тела находится затем как F / a: достаточно знать ускорение при каком-то одном значении силы.

В 2018 году учёные заменили эталон килограмма, хранящийся в Международном бюро мер и весов во Франции с 1889 года. Теперь единица массы определяется с помощью постоянной Планка. Для создания нового эталона массы применяются весы Киббла — устройство, которое определяет, какой ток нужен для того, чтобы создать электромагнитное поле, способное уравновесить чашу с тестируемым эталоном^[8]. Старый эталон отныне играет роль очень точной гири.

По своему смыслу гравитационная масса — характеристика тел в классической механике, являющаяся мерой их гравитационного взаимодействия

${\displaystyle F_{gr}=G{\frac {m_{1}m_{2}}{r^{2}}},}$

где G — гравитационная постоянная (константа Ньютона), r — расстояние между материальными точками, обладающими гравитационными массами ${\displaystyle m_{1}}$ и ${\displaystyle m_{2}}$.

Первая проверка пропорциональности гравитационной и инертной масс была выполнена Галилеем, изучавшим свободное падение. Согласно опытам Галилея, все тела, независимо от их массы и материала, падают с одинаковым ускорением. Сейчас эти опыты можно трактовать так, что увеличение силы, действующей на более массивное тело со стороны гравитационного поля Земли, полностью компенсируется увеличением его инертных свойств. Позднее на пропорциональность двух видов массы обратил внимание Ньютон, он же впервые доказал, что эта пропорциональность выдерживается с точностью не хуже 0,1 %^[9].

С учётом сказанного раздельных единиц для гравитационной и инертной массы не вводят, а коэффициент их пропорциональности принят равным 1 с надлежащим подбором константы G. На сегодня пропорциональность (условно говоря, «равенство масс») экспериментально проверена с очень высокой точностью: чувствительность к относительной разности в лучшем эксперименте на 2009 год^[5][6] имеет порядок 10⁻¹³.

Подобные эксперименты привели к формулированию принципа эквивалентности:

Все явления в гравитационном поле происходят точно так же, как в соответствующем поле сил инерции, если совпадают напряжённости этих полей и одинаковы начальные условия для тел системы.

имеющего два уровня глобальности охвата «всех явлений». Так называемый «сильный» принцип гласит: в каждой точке пространства-времени в произвольном гравитационном поле можно выбрать локально-инерциальную систему координат, такую, что в достаточно малой окрестности рассматриваемой точки законы природы будут иметь такую же форму, как и в неускоренных декартовых системах координат, где под «законами природы» подразумевают все законы природы. «Слабый» принцип отличается заменой слов «законы природы» словами «законы движения свободно падающих частиц». Слабый принцип — это не что иное, как другая формулировка наблюдаемого равенства гравитационной и инертной масс, в то время как сильный принцип представляет собой обобщение наблюдений за влиянием гравитации на любые физические объекты.

В Международной системе единиц (СИ) масса измеряется в килограммах. Единицей измерения массы в системе СГС является грамм (1⁄1000 килограмма). Вообще говоря, в любой системе измерения выбор основных (первичных) физических величин, их единиц измерения и их числа произволен — зависит от принимаемого соглашения и масса не всегда входит в их состав — так в системе МКГСС единица массы была производной единицей и измерялась в кГс·с²/м (называлась «техническая единица массы» или «инерта»). В атомной физике и химии принято сравнивать [соотносить] массу с относительной атомной массой (а.е.м.), в физике твёрдого тела — с массой электрона (Атомная система единиц), в физике элементарных частиц массу измеряют в электронвольтах. Кроме этих единиц, используемых в науке, существует большое разнообразие исторических единиц измерения массы, которые сохранили свою отдельную сферу использования: фунт, унция, карат, тонна и др. В астрофизике единицей для сравнения масс небесных тел служит масса Солнца.

В некоторых естественных системах единиц в качестве единицы массы используются массы элементарных частиц: электрона или протона^[10]. В планковской системе единиц, также относящейся к естественным системам, единицей массы является планковская масса.

Массы очень мелких частиц могут быть определены с помощью величины, обратной к комптоновской длине волны: 1 см^-1 ≈ 3,52⋅10⁻⁴¹ кг. Масса очень большой звезды или чёрной дыры может быть отождествлена с её гравитационным радиусом: 1 см ≈ 6,73⋅10²⁴ кг.

Масса — одна из важнейших величин в физике. Это скалярная неотрицательная релятивистски инвариантная величина. По современным представлениям, масса эквивалентна энергии покоя (mc², где c — скорость света в вакууме). Масса входит в выражения кинетической энергии (mv²/2, где v — скорость) и импульса (mv) материальной точки.

Масса тела, выраженная в килограммах, численно примерно равна весу этого тела, выраженному в кгс (1 кгс ≈ 10 Н), когда оно покоится вблизи поверхности Земли. Поэтому в повседневных ситуациях слово «вес» нередко синонимизируется со словом «масса». Однако это разные понятия, и в общем случае численные значения массы и веса не совпадают, не говоря уже о различии размерностей. Например, при помещении предмета на обычные магазинные весы показания колеблются в течение нескольких секунд: в это время вес претерпевает изменения, а масса постоянна. Также возможны ситуации с нулевым весом и ненулевой массой одного и того же тела: в условиях невесомости вес всех тел равен нулю, а масса у каждого тела своя.

В классической механике масса инвариантна относительно смены системы отсчёта и аддитивна, то есть масса системы тел равна сумме масс составляющих её тел.

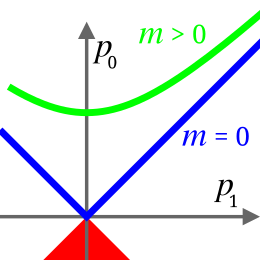
Наиболее строгое определение массы даётся в специальной теории относительности (СТО): масса — это абсолютная величина 4-вектора энергии-импульса^[11]:

${\displaystyle m^{2}={\frac {E^{2}}{c^{4}}}-{\frac {\mathbf {p} ^{2}}{c^{2}}},}$

где E — полная энергия свободного тела, p — его 3-импульс, c — скорость света. В СТО масса является неаддитивной, но, как и в классической физике, инвариантной величиной.

В случае произвольной метрики пространства-времени (как в общей теории относительности) это определение требует некоторого обобщения:

${\displaystyle m^{2}={1 \over c^{2}}g_{ik}p^{i}p^{k}.}$

Здесь ${\displaystyle g_{ik}}$ — метрический тензор, ${\displaystyle p^{i}}$ — 4-импульс.

Определённая выше масса является релятивистским инвариантом, то есть она одна и та же во всех системах отсчёта. Если перейти в систему отсчёта, где тело покоится, то ${\displaystyle m={\tfrac {E_{0}}{c^{2}}}}$ — масса определяется энергией покоя (Эквивалентность массы и энергии).

Особенно просто выглядят эти определения в системе единиц, в которой за единицу измерения скорости принята скорость света (например, в планковской или же в принятой в физике элементарных частиц для описания процессов при высоких энергиях релятивистской системе единиц, в которой масса, импульс и энергия имеют размерность энергии^[12] и измеряются в электронвольтах):

В СТО: ${\displaystyle m={\sqrt {p_{i}^{2}}}={\sqrt {E^{2}-\mathbf {p} ^{2}}}.}$

В ОТО: ${\displaystyle m={\sqrt {g_{ik}p^{i}p^{k}}}.}$

Частицы с нулевой массой (фотон и гипотетический гравитон) двигаются в вакууме со скоростью света (c ≈ 300 000 км/с), и поэтому не существует системы отсчёта, в которой бы они покоились. Напротив, частицы с ненулевой массой всегда движутся медленнее скорости света.

В современной терминологии термин масса применяется вместо терминов инвариантная масса или масса покоя, являясь полностью эквивалентным им по смыслу. В некоторых ситуациях (особенно в популярной литературе) это, однако, уточняется явно, чтобы избежать путаницы из-за понимания термина масса в другом — устаревшем — смысле, описанном в этом подразделе.

В большом количестве источников^[13][14], относящихся к началу и середине XX века, а также в научно-популярных^[15], введённое выше понятие массы называли «массой покоя», при этом саму массу вводили на основе классического определения импульса

${\displaystyle \mathbf {p} =m\mathbf {v} .}$

В таком случае ${\displaystyle m={\tfrac {E}{c^{2}}}}$, и поэтому говорили, что масса тела растёт с увеличением скорости. При таком определении понятие массы было эквивалентно понятию энергии, а также требовалось отдельно вводить «массу покоя», измеряемую в собственной СО, и «релятивистскую массу» движущегося тела. Такой подход был распространён в течение длительного времени^[15] и позволял провести многочисленные аналогии с классической физикой, однако в современной научной литературе используется редко^[16], так как вносит дополнительную путаницу в терминологию, не давая никаких новых результатов. Так называемая релятивистская масса оказывается аддитивной (в отличие от массы покоя системы, зависящей от состояния составляющих её частиц). Однако безмассовые частицы (например, фотоны) в такой терминологии оказываются имеющими переменную массу; кроме того, релятивистская масса ничуть не упрощает формулировку законов динамики частиц.

Полным аналогом классического определения импульса через массу и скорость в СТО следует считать ковариантное равенство

${\displaystyle P_{\mu }=mu_{\mu },}$

где m — инвариантная масса, а u_μ — 4-скорость (производная от 4-координаты по собственному времени частицы ${\displaystyle dr_{\mu }/d\tau }$; единичный вектор, направленный вдоль мировой линии частицы).

Также можно записать ковариантный эквивалент второго закона Ньютона:

${\displaystyle F_{\mu }=ma_{\mu },}$

где ${\displaystyle a_{\mu }=du_{\mu }/d\tau }$ — 4-ускорение (кривизна мировой линии частицы).

В релятивистской механике, в отличие от классической, масса не является аддитивной физической величиной, то есть масса системы в общем случае не равна сумме масс её компонентов. Масса системы зависит от характера движения частиц друг относительно друга и в случае взаимодействующих частиц также включает в себя энергию связи^{[Комм 1]}.

Масса устойчивой системы взаимодействующих частиц, совершающих финитное движение (например, нуклонов в атомном ядре), может зависеть от внутреннего состояния этой системы. Она меньше суммы масс частиц на величину ${\displaystyle E_{b}/c^{2},}$ называемую дефектом массы, где ${\displaystyle E_{b}}$ — энергия связи системы, ${\displaystyle c}$ — скорость света^[17].

Масса системы невзаимодействующих релятивистских частиц не меньше суммы их масс и равна данной сумме, только когда все частицы покоятся друг относительно друга^[18]. Это утверждение следует из того, что в релятивистской механике массой системы частиц называется модуль её четырёхимпульса^[19]: ${\displaystyle M={\sqrt {E^{2}-{\vec {p}}^{2}}}.}$ В системе отсчёта, для которой полный пространственный импульс системы частиц равен нулю ${\displaystyle {\vec {p}}=0,}$ для системы невзаимодействующих частиц, в силу аддитивности энергии, получаем ${\displaystyle M=E=\sum _{\alpha }E_{\alpha }=\sum _{\alpha }{\sqrt {m_{\alpha }^{2}+{\vec {p}}_{\alpha }^{2}}}}$ (индекс ${\displaystyle \alpha }$ нумерует частицы). Иными словами, ${\displaystyle M\geqslant \sum _{\alpha }m_{\alpha },}$ причём равенство левой и правой частей обеспечивается, только когда все ${\displaystyle {\vec {p}}_{\alpha }}$ равны нулю.

Для системы, подверженной распаду (например, радиоактивному), величина энергии покоя определена лишь с точностью до постоянной Планка, делённой на время жизни: ${\displaystyle \Delta mc^{2}\approx \hbar /\tau .}$ При описании такой системы при помощи квантовой механики удобно считать массу комплексной, с мнимой частью, равной означенному Δm.

Масса частиц микромира

Масса всех известных на сей день частиц является неотрицательной величиной. В физике элементарных частиц понятие массы чрезвычайно важно, так как позволяет отделять безмассовые частицы (всегда двигающиеся со скоростью света, как фотоны) от массивных (скорость которых всегда ниже скорости света).

Кроме того, масса практически однозначно позволяет идентифицировать частицу (с точностью до зарядового сопряжения, меняющего частицы и античастицы). Наличие массы у кварков и лептонов объясняется их взаимодействием с полем Хиггса, и чем сильнее это взаимодействие, тем больше масса^[20][21]. Масса элементарной частицы постоянна, она одинакова у всех частиц данного типа и их античастиц. В то же время в физике элементарных частиц рассматриваются объекты без определённой массы (которые также можно называть элементарными частицами); эти частицы являются линейными квантовомеханическими комбинациями частиц, имеющих определённую массу (массовых состояний). Так, нейтрино с определёнными флейворами (то есть электронное, мюонное и тау-нейтрино и соответствующие им антинейтрино) не имеют определённых масс, и наоборот, массовые состояния нейтрино не обладают определёнными флейворами, а являются смесью флейворных состояний; этот факт является причиной нейтринных осцилляций. То же относится и к ряду нейтральных мезонов (K⁰, B⁰- и D⁰-мезоны). В частности, K0
и K0
-мезоны, являющиеся собственными состояниями гамильтониана сильного взаимодействия, не обладают, строго говоря, определённой массой (и временем жизни), будучи суперпозицией двух массовых состояний K0
S и K0
L (см. Смешивание нейтральных каонов); однако разность масс m(K0
S) − m(K0
L) = 3,5·10⁻⁶ эВ настолько мала по сравнению с их массой m_K ≈ m(K0
S) ≈ m(K0
L) ≈ 497,611 МэВ и даже с экспериментальной погрешностью её измерения (13 кэВ), что можно считать массу каона K0
и антикаона K0
определённой и равной m_K^[22].

Положительная масса

К частицам с положительной массой (тардионам) относятся почти все частицы Стандартной модели: лептоны (включая нейтрино, которые в первоначальной версии Стандартной модели считались безмассовыми), кварки, W- и Z-бозоны, бозон Хиггса. Эти частицы могут двигаться с любой скоростью, меньшей скорости света, в том числе покоиться. К тардионам относятся также все известные составные частицы: барионы (в том числе протон и нейтрон) и мезоны.

Нулевая масса

К известным на сегодняшний день частицам нулевой массы (безмассовым, люксонам) относятся фотоны и глюоны, а также гипотетические гравитоны. Такие частицы в свободном состоянии могут двигаться только со скоростью света. Но поскольку из квантовой хромодинамики следует, что глюоны в свободном состоянии не существуют, то непосредственно наблюдать движущимися со скоростью света можно только фотоны (собственно, именно поэтому говорят о «скорости света»). Долгое время считалось, что нейтрино также имеют нулевую массу, однако обнаружение вакуумных нейтринных осцилляций свидетельствует о том, что масса нейтрино хоть и очень мала, но не равна нулю.

Комбинация нескольких частиц нулевой массы может (а в случае, например, сцепленных частиц — должна) иметь ненулевую массу.

Отрицательная масса

Частицы с отрицательной массой двигались бы с любой скоростью, меньшей скорости света, аналогично тардионам, и имели бы отрицательную энергию и импульс, направленный в сторону, противоположную направлению движения. Допущение существования отрицательных масс ведёт к определённым сложностям в интерпретации принципа эквивалентности и закона сохранения импульса. В то же время в общей теории относительности допускается существование локальных пространственных областей с отрицательной плотностью энергии-импульса. В частности, подобную область можно создать с помощью эффекта Казимира^[23].

Мнимая масса

В рамках специальной теории относительности математически возможно существование частиц с мнимой массой, так называемых тахионов. Такие частицы будут иметь реальные значения энергии и импульса, а их скорость должна всегда быть выше скорости света. Однако допущение возможности наблюдения одиночных тахионов вызывает ряд методологических трудностей (например, нарушение принципа причинности), поэтому в большинстве современных теорий одиночные тахионы не вводятся. Впрочем, в квантовой теории поля мнимая масса может быть введена для рассмотрения тахионной конденсации, не нарушающей принцип причинности.

Большинство приборов для измерения массы основано на использовании принципа эквивалентности инертной и гравитационной массы. С помощью таких приборов, называемых весами, массу тел определяют по их весу. В пружинных весах вес измеряется по степени деформации гибкой пружины. В рычажных — вес определяется путём сравнения веса интересующего тела с весом эталонов (гирь) известной массы.

Однако в ситуации невесомости (скажем, на космических станциях) весы неприменимы, и используются другие устройства — массметры, действие которых основано на измерении периода свободных колебаний груза на пружине; этот период, как известно, зависит от массы тела.

Массы заряженных элементарных частиц определяют по их следам в камере Вильсона^[24]. Массы короткоживущих элементарных частиц, не оставляющих следов в камере Вильсона, определяют, оценивая суммарную энергию продуктов их распада^[25][26].

Массу Земли определяют на основе закона всемирного тяготения Ньютона, исходя из известных значений гравитационной постоянной и радиуса Земли^[27]. Массу Солнца определяют также на основе закона всемирного тяготения Ньютона, исходя из известных значений гравитационной постоянной, расстояния между Землёй и Солнцем и периода обращения Земли вокруг Солнца^[28]. Масса нашей Галактики определяется исходя из периода обращения окрестностей Солнца вокруг центра Галактики и расстояния до центра Галактики^[29].

Массы ближайших двойных звёзд определяются по расстоянию между ними и периоду их обращения. Если звезда не имеет спутника и принадлежит главной последовательности, то её массу можно определить исходя из её светимости или температуры поверхности^[30].

Объект	Масса (кг)	В других единицах
Нейтрино	< 1,5⋅10−37	< 0,12	эВ
Электрон	9,1⋅10−31	5,1⋅105	эВ
Протон	1,7⋅10−27	9,4⋅108	эВ
Бозон Хиггса	2,4⋅10−25	1,3⋅1011	эВ
Вирус гриппа	6⋅10−19	4⋅108	а.е.м.
Снежинка	1⋅10−7	0,1	мг
Человек	80	176	фунт
Слон	4,5⋅103	4,5	тонн
Кит	1,5⋅105	150	тонн
Пирамида Хеопса	6,0⋅109	6,0⋅106	тонн
Земля	6,0⋅1024	${\displaystyle 1}$	масс Земли
Юпитер	1,9⋅1027	${\displaystyle 314}$	масс Земли
Солнце	2,0⋅1030	${\displaystyle 1}$	масс Солнца
Другие звёзды	4,0⋅1028—1,8⋅1032	0,02—90	масс Солнца
Наша Галактика	2,6⋅1041	1,3⋅1011	масс Солнца
Другие галактики	2,0⋅1036—2,0⋅1043	106—1013	масс Солнца

Слово масса (лат. massa, от др.-греч. μαζα) первоначально в античные времена обозначало кусок теста. Позднее смысл слова расширился, и оно стало обозначать цельный, необработанный кусок произвольного вещества; в этом смысле слово используется, например, у Овидия и Плиния^[31]. В ряде областей науки и техники это слово (часто во множественном числе) до сих пор продолжает использоваться в значении какой-либо относительно однородной субстанции (воздушные массы, пластмасса, бумажная масса, селевая масса, народные массы).

Масса как научный термин для меры количества вещества была введена Ньютоном, до этого естествоиспытатели оперировали понятием веса. В труде «Математические начала натуральной философии» (1687) Ньютон сначала определил «количество материи» в физическом теле как произведение его плотности на объём. Далее он указал, что в том же смысле будет использовать термин масса. Наконец, Ньютон ввёл массу в законы физики: сначала во второй закон Ньютона (через количество движения), а затем — в закон тяготения, откуда сразу следует, что вес пропорционален массе^[32]. Ньютон явно указал на эту пропорциональность и даже проверил её на опыте со всей возможной в те годы точностью: «Определяется масса по весу тела, ибо она пропорциональна весу, что мной найдено опытами над маятниками, произведёнными точнейшим образом»^[33] (эти опыты Ньютон подробно описал в III томе своих «Начал»).

Фактически Ньютон использует только два понимания массы: как меры инерции и источника тяготения^[34]. Толкование её как меры «количества материи» — не более чем наглядная иллюстрация, оно сохранялось в XVII—XIX веке, но затем подверглось критике как нефизическое и бессодержательное^[35]. В настоящее время понятие «количество вещества» применяется, но имеет совершенно другой смысл.

Долгое время одним из главных законов природы считался закон сохранения массы. Однако в XX веке выяснилось, что этот закон является ограниченным вариантом закона сохранения энергии и во многих ситуациях не соблюдается.

Прямые обобщения понятия массы включают в себя такие тензорные характеристики, как момент инерции, и такие показатели свойств системы «тело плюс среда», как массовое водоизмещение, присоединённая масса и эффективная масса, используемые в гидростатике, гидродинамике и квантовой теории.

Например, введение так называемой эффективной массы позволяет учесть взаимодействие электрона (или дырки) с периодическим электромагнитным полем кристаллической решётки в полупроводнике, что необходимо для корректного квантовомеханического описания движения носителей заряда.

• Эквивалентность массы и энергии
• Принцип эквивалентности сил гравитации и инерции
• Скрытая масса
• Сравнение массы и веса
• Эффективная масса

• Джеммер, Макс. Понятие массы в классической и современной физике. — М.: Прогресс, 1967.
  • Переиздание: Едиториал УРСС, 2003, ISBN 5-354-00363-6.
• Окунь Л. Б. Понятие массы (Масса, энергия, относительность) Успехи физических наук, № 158 (1989)
• Окунь Л. Б. О письме Р. И. Храпко «Что есть масса?». Успехи физических наук, № 170, с.1366 (2000)
• L. B. Okun. On the concepts of vacuum and mass and the search for higgs (англ.) // Modern Physics Letters A. — 2012. — Vol. 27. — P. 1230041. — doi:10.1142/S0217732312300418. — arXiv:1212.1031.
• Спасский Б. И.. История физики. М., «Высшая школа», 1977. Том 1, часть 1-я.
• Gordon Kane. The Mysteries of Mass. // Scientific American. June 27, 2005.
• Завельский Ф. С. Взвешивание миров, атомов и элементарных частиц. — М.: Атомиздат, 1970. — 176 с.

• Государственный первичный эталон единицы массы ГЭТ 3-2008

В статье есть список источников, но не хватает сносок. Без сносок сложно определить, из какого источника взято каждое отдельное утверждение. Вы можете улучшить статью, проставив сноски на источники, подтверждающие информацию. Сведения без сносок могут быть удалены. (19 марта 2016)