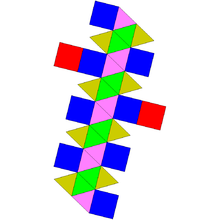
Скрученно удлинённый четырёхскатный бикупол
| Скрученно удлинённый четырёхскатный бикупол | |||
|---|---|---|---|
 «Правый» вариант (3D-модель) | |||
| Тип | многогранник Джонсона | ||
| Свойства | выпуклый, хиральный | ||
| Комбинаторика | |||
| Элементы |
|
||
| Грани |
24 треугольника 10 квадратов |
||
| Конфигурация вершины |
8(3.43) 2x8(34.4) |
||
|
|
|||
| Классификация | |||
| Обозначения | J45, М5+А8+М5 | ||
| Группа симметрии | D4 | ||
Скру́ченно удлинённый четырёхска́тный бику́пол[1] — один из многогранников Джонсона (J45, по Залгаллеру — М5+А8+М5).
Составлен из 34 граней: 24 правильных треугольников и 10 квадратов. Среди квадратных граней 2 окружены четырьмя квадратными, остальные 8 — квадратной и тремя треугольными; среди треугольных граней 8 окружены двумя квадратными и треугольной, 8 — квадратной и двумя треугольными, 8 — тремя треугольными.
Имеет 56 рёбер одинаковой длины. 8 рёбер располагаются между двумя квадратными гранями, 24 — между квадратной и треугольной, остальные 24 — между двумя треугольными.
У скрученно удлинённого четырёхскатного бикупола 24 вершины. В 8 вершинах сходятся три квадратных и треугольная грани; в остальных 16 — квадратная и четыре треугольных.
Скрученно удлинённый четырёхскатный бикупол можно получить из двух четырёхскатных куполов (J4) и правильной восьмиугольной антипризмы, все рёбра у которой равны, — приложив восьмиугольные грани куполов к основаниям антипризмы.
Это один из пяти хиральных многогранников Джонсона (наряду с J44, J46, J47 и J48), существующих в двух разных зеркально-симметричных (энантиоморфных) вариантах — «правом» и «левом».
-
«Правый» вариант
-
«Левый» вариант
Кроме того, среди многогранников Джонсона это единственный с группой симметрии D4.
Метрические характеристики
Если cкрученно удлинённый четырёхскатный бикупол имеет ребро длины , его площадь поверхности и объём выражаются как
Примечания
- ↑ Залгаллер В. А. Выпуклые многогранники с правильными гранями / Зап. научн. сем. ЛОМИ, 1967. — Т. 2. — Cтр. 22.
Ссылки
- Weisstein, Eric W. Скрученно удлинённый четырёхскатный бикупол (англ.) на сайте Wolfram MathWorld.